6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
2 participantes
Página 1 de 1.
 6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
Redacción BBC News Mundo
https://www.bbc.com/mundo/noticias-49168226
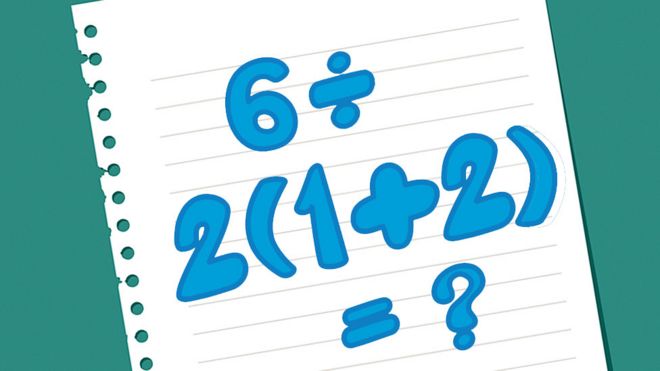 Image caption ¿Cuál es la respuesta correcta?
Image caption ¿Cuál es la respuesta correcta?
A ver: inténtalo. ¿Cuánto es 6 ÷ 2(1+2)?
Quizás hayas solucionado este problema matemático antes, en una de las varias veces que ha circulado por las redes sociales, generando discusiones acaloradas entre los defensores de diferentes opiniones.
Lo curioso es que, generalmente, la aritmética no es un asunto que depende de tu punto de vista: no importa cómo lo mires, 1 + 1 es 2.
Sólo que, en este caso, desde expertos hasta entusiastas -y probablemente tú- responden que:
6 ÷ 2(1+2) = 1.
Saltar las recomendacionesQuizás también te interese
Fin de las recomendaciones.
O que:
6 ÷ 2(1+2) = 9.
Y cada bando cuenta con decenas de millones de fervientes defensores, a juzgar por la cantidad de videos publicados en la web articulando los pasos para llegar a 1 o 9, algunos con vistas en el rango de 3 a 5 millones.
¿Cómo puede ser posible?
 Image caption Hay un orden establecido: 1. Paréntesis; 2. Potencias y Raíces ; 3. Multiplicaciones y Divisiones; 4. Sumas y Restas, estas dos últimas en el orden en que se encuentren, de izquierda a derecha.
Image caption Hay un orden establecido: 1. Paréntesis; 2. Potencias y Raíces ; 3. Multiplicaciones y Divisiones; 4. Sumas y Restas, estas dos últimas en el orden en que se encuentren, de izquierda a derecha.
El orden de operaciones es una convención y dice que debes de ir de izquierda a derecha evaluando primero los paréntesis.
Luego resuelves la potenciación y raíces, antes de hacer todas las multiplicaciones y divisiones.
Al final, sumas y restas.
Para ayudar a recordar este orden, hay dos acrónimos:
Armados con estas instrucciones, volvamos lo que nos ocupa.
Entonces sumamos 1 + 2 y queda 6 ÷ 2(3);
Paso seguido, multiplicamos 2 x 3 , lo que nos da 6.
Ahora sí, con todo lo que tenía que ver con el paréntesis resuelto, solo queda 6 ÷ 6 = 1.
Aunque quizás lo resolviste así:
6 ÷ 2(1+2): multiplicas lo que está dentro del paréntesis por el 2 que está afuera, quedando
6 ÷ (2+4) = 6 ÷ 6 = 1.
¿O será que se refiere a resolver todo lo que está entre paréntesis?
De ser así, 6 ÷ 2(1+2) = 6 ÷ 2(3) = 6 ÷ 2 x 3
Entonces dividimos 6 por 2 = 3 y lo multiplicamos por 3 = 9.
 Image caption Los dos parecen correctos...
Image caption Los dos parecen correctos...
¿Cuál de los resultados es correcto: 1 o 9?
Inusualmente ambos.
El problema 6 ÷ 2(1+2) destaca la diferencia entre esas interpretaciones.
"No hay un estándar: ambas son sustancialmente populares en todo el mundo", indica el experto.
Es por eso que ninguna de las dos soluciones es errada: todo depende de cómo te enseñaron a resolver el problema.
Hay quienes aprendieron que se debe resolver lo que está entre paréntesis primero y que "a(b) siempre es intercambiable con a x b" o, en este caso, que 2(3) es lo mismo que 2 x 3. Así que al escribir 6 ÷ 2 x 3 la respuesta efectivamente es 9.
A otros les enseñaron que hay que solucionar lo que involucre los paréntesis y que "a(b) siempre es intercambiable con (ab)", y concluyen que la solución es 1.
 Image caption Ambos están bien... o ambos están mal: ninguno, hasta ahora, es más correcto que el otro.
Image caption Ambos están bien... o ambos están mal: ninguno, hasta ahora, es más correcto que el otro.
"Aunque muchos problemas en matemáticas son eventualmente resueltos por un individuo o un equipo que proporciona una prueba decisiva, en este caso parece muy poco probable que concluya así pues no es un problema puramente matemático: es parcialmente un problema de comunicación", agrega.
La solución sería fácil si alguno de los dos bandos fuera obviamente más numeroso que el otro pero ambas interpretaciones son sustancialmente populares en todo el mundo.
A falta de un consenso, y dado que "se trata de una cuestión de comunicación, no de matemáticas, seguirá teniendo dos (o ninguna) respuestas numéricas aceptables".
Eso naturalmente provoca un animado debate, de manera que seguramente 6 ÷ 2(1+2) continuará disfrutando de popularidad cíclica en las redes.
Lo que hay que tener claro, subraya el matemático puro, es que "puedes decir que la respuesta es 1, y es correcto; puedes decir que la respuesta es 9, y es correcto. Pero si dices que una de esas dos respuestas es incorrecta, el que está errado eres tú".
Redacción BBC News Mundo
- 4 horas
https://www.bbc.com/mundo/noticias-49168226
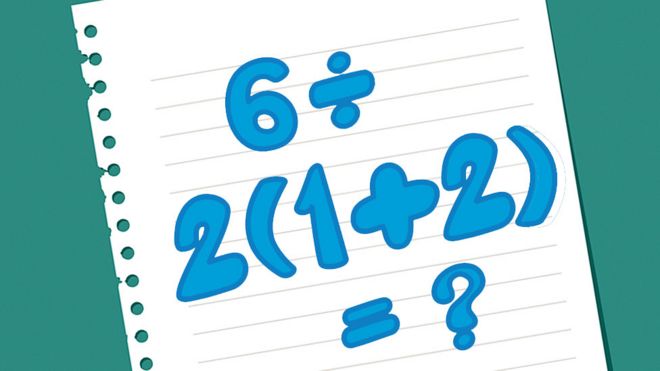 Image caption ¿Cuál es la respuesta correcta?
Image caption ¿Cuál es la respuesta correcta?A ver: inténtalo. ¿Cuánto es 6 ÷ 2(1+2)?
Quizás hayas solucionado este problema matemático antes, en una de las varias veces que ha circulado por las redes sociales, generando discusiones acaloradas entre los defensores de diferentes opiniones.
Lo curioso es que, generalmente, la aritmética no es un asunto que depende de tu punto de vista: no importa cómo lo mires, 1 + 1 es 2.
Sólo que, en este caso, desde expertos hasta entusiastas -y probablemente tú- responden que:
6 ÷ 2(1+2) = 1.
Saltar las recomendacionesQuizás también te interese
- Quién es la "Princesa de la Ciencia" y cómo busca alentar a las mujeres a ser científicas
- La curiosa historia de la isla de Ocracoke, el único lugar de Estados Unidos donde no se habla inglés americano
- ¡Deja de tratar de ser feliz! No estamos diseñados para serlo
- La caja de Pandora que destapó el cándido botón “me gusta” de Facebook
.wsoj-component .parrot__title { margin-bottom: 0 }
Fin de las recomendaciones.
O que:
6 ÷ 2(1+2) = 9.
Y cada bando cuenta con decenas de millones de fervientes defensores, a juzgar por la cantidad de videos publicados en la web articulando los pasos para llegar a 1 o 9, algunos con vistas en el rango de 3 a 5 millones.
¿Cómo puede ser posible?
¡Orden!
Para desentrañar esta materia, desempolvemos el manual de instrucciones sobre el orden en el que se debe realizar cada operación en un problema matemático. Image caption Hay un orden establecido: 1. Paréntesis; 2. Potencias y Raíces ; 3. Multiplicaciones y Divisiones; 4. Sumas y Restas, estas dos últimas en el orden en que se encuentren, de izquierda a derecha.
Image caption Hay un orden establecido: 1. Paréntesis; 2. Potencias y Raíces ; 3. Multiplicaciones y Divisiones; 4. Sumas y Restas, estas dos últimas en el orden en que se encuentren, de izquierda a derecha.El orden de operaciones es una convención y dice que debes de ir de izquierda a derecha evaluando primero los paréntesis.
Luego resuelves la potenciación y raíces, antes de hacer todas las multiplicaciones y divisiones.
Al final, sumas y restas.
Para ayudar a recordar este orden, hay dos acrónimos:
- papomudas por «paréntesis, potencias, multiplicación, división, adición, sustracción» y
- papomudisure por «paréntesis, potencias, multiplicación, división, suma, resta».
Armados con estas instrucciones, volvamos lo que nos ocupa.
Vamos por pasos
Partiendo de 6 ÷ 2(1+2), debemos ocuparnos primero de todo lo que tiene que ver con los paréntesis, como indica papomudas.Entonces sumamos 1 + 2 y queda 6 ÷ 2(3);
Paso seguido, multiplicamos 2 x 3 , lo que nos da 6.
Ahora sí, con todo lo que tenía que ver con el paréntesis resuelto, solo queda 6 ÷ 6 = 1.
Aunque quizás lo resolviste así:
6 ÷ 2(1+2): multiplicas lo que está dentro del paréntesis por el 2 que está afuera, quedando
6 ÷ (2+4) = 6 ÷ 6 = 1.
¿O será que se refiere a resolver todo lo que está entre paréntesis?
De ser así, 6 ÷ 2(1+2) = 6 ÷ 2(3) = 6 ÷ 2 x 3
Entonces dividimos 6 por 2 = 3 y lo multiplicamos por 3 = 9.
 Image caption Los dos parecen correctos...
Image caption Los dos parecen correctos...¿Cuál de los resultados es correcto: 1 o 9?
Inusualmente ambos.
Depende de cómo te lo enseñaron
Lo que pasa es que "hay dos interpretaciones ligeramente diferentes de papomudas (o papomudisure)", señala el matemático puro David Linkletter en su artículo "The PENDAS paradox" publicado por +plus magazine.El problema 6 ÷ 2(1+2) destaca la diferencia entre esas interpretaciones.
"No hay un estándar: ambas son sustancialmente populares en todo el mundo", indica el experto.
Es por eso que ninguna de las dos soluciones es errada: todo depende de cómo te enseñaron a resolver el problema.
Hay quienes aprendieron que se debe resolver lo que está entre paréntesis primero y que "a(b) siempre es intercambiable con a x b" o, en este caso, que 2(3) es lo mismo que 2 x 3. Así que al escribir 6 ÷ 2 x 3 la respuesta efectivamente es 9.
A otros les enseñaron que hay que solucionar lo que involucre los paréntesis y que "a(b) siempre es intercambiable con (ab)", y concluyen que la solución es 1.
 Image caption Ambos están bien... o ambos están mal: ninguno, hasta ahora, es más correcto que el otro.
Image caption Ambos están bien... o ambos están mal: ninguno, hasta ahora, es más correcto que el otro.¿Pero y entonces?
En un escrito más detallado sobre el tema, Linkletter señala: "Matemáticamente, es inconsistente creer simultáneamente que a(b) es intercambiable con a x b y también que a(b) es intercambiable con (ab), porque entonces se deduce que 1 = 9"."Aunque muchos problemas en matemáticas son eventualmente resueltos por un individuo o un equipo que proporciona una prueba decisiva, en este caso parece muy poco probable que concluya así pues no es un problema puramente matemático: es parcialmente un problema de comunicación", agrega.
La solución sería fácil si alguno de los dos bandos fuera obviamente más numeroso que el otro pero ambas interpretaciones son sustancialmente populares en todo el mundo.
A falta de un consenso, y dado que "se trata de una cuestión de comunicación, no de matemáticas, seguirá teniendo dos (o ninguna) respuestas numéricas aceptables".
Eso naturalmente provoca un animado debate, de manera que seguramente 6 ÷ 2(1+2) continuará disfrutando de popularidad cíclica en las redes.
Lo que hay que tener claro, subraya el matemático puro, es que "puedes decir que la respuesta es 1, y es correcto; puedes decir que la respuesta es 9, y es correcto. Pero si dices que una de esas dos respuestas es incorrecta, el que está errado eres tú".
_________________


Azali- Admin
- Cantidad de envíos : 50980
Fecha de inscripción : 27/10/2008
 Re: 6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
Re: 6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
Entonces el resultado depende de lo que a uno le dé la gana, así que para Azali será según le enseñó Fidel. Ella sabrá si es 1 o es 9.

Sócrates- Admin
- Cantidad de envíos : 11527
Fecha de inscripción : 18/03/2009

Azali- Admin
- Cantidad de envíos : 50980
Fecha de inscripción : 27/10/2008
 Re: 6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
Re: 6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
Si Fidel dice que es 1 es que es 1.

Sócrates- Admin
- Cantidad de envíos : 11527
Fecha de inscripción : 18/03/2009
 Re: 6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
Re: 6 ÷ 2(1+2): Por qué la solución a esta sencilla ecuación es tan problemática
Cenicitas no puede decir ni hostias!
_________________


Azali- Admin
- Cantidad de envíos : 50980
Fecha de inscripción : 27/10/2008
Contenido patrocinado
 Temas similares
Temas similares» Azali encuentra solución a su problema
» Ecuación Siniestra
» ¿Es una ecuación de Luik?
» Algún día .. no tendrá solución.
» Solución del conflicto con el canal de Panamá
» Ecuación Siniestra
» ¿Es una ecuación de Luik?
» Algún día .. no tendrá solución.
» Solución del conflicto con el canal de Panamá
Página 1 de 1.
Permisos de este foro:
No puedes responder a temas en este foro.

